Table of Contents
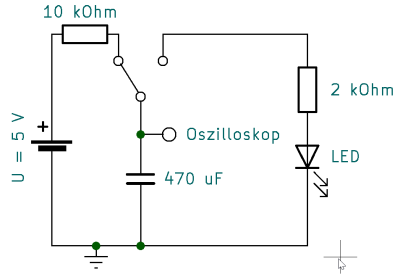
Versuch: Lade- und Entladevorgang
- Bei der linken Schalterstellung wird der Kondensator über den $10\,\mathrm{k\Omega}$-Widerstand aufgeladen.
- Wird der Schalter dann nach rechts umgeschaltet, so entlädt sich der Kondensator über den $2\,\mathrm{k\Omega}$-Widerstand und die LED.
Wir wollen den Zeit-Spannungs-Graphen mit dem Oszilloskop aufzeichnen. Stelle das Oszilloskop dazu folgendermaßen ein:
- Horizontale Auflösung: 2V/Div
- Vertikale Auflösung: 5 s/Div
- Vertikaler Triggerpunkt: < 0V
- Horizontaler Triggerpunkt: ganz links
Drücke dann auf den Knopf “Single”, damit nur 1-mal getriggert wird. Da keine negative Spannung erreicht wird, triggert das Oszilloskop jetzt nicht automatisch, sondern nur, wenn Du es mit dem Button “Force” erzwingst. Daher gehen wir jetzt wie folgt vor:
- Schalter auf rechte Schalterstellung bringen und warten, bis der Kondensator entladen ist.
- Am Oszilloskop auf “Force” drücken
- Schalter auf linke Schalterstellung und warten, bis der Kondensator fast komplett aufgeladen ist.
- Schalter auf rechte Schalterstellung und warten, bis der Kondensator sich fast komplett entladen hat.
Bei den letzten beiden Punkten “schreibt” das Oszilloskop mit. Baut man anstatt der LED und dem 2 kOhm-Widerstand einen zweiten 10 kOhm-Widerstand ein, so sieht der t-U-Graph am Oszilloskop so aus:

Um die Wirkung des Kondensators zu veranschaulichen, gibt es eine schöne Schaltungsvariante: Verwende statt des 10 kOhm-Widerstands einen 1 kOhm-Widerstand zum Laden und schalte in den Ladekreis eine zweite LED. Was beobachtest Du beim Laden/Entladen?
Zeitlicher Verlauf
Zum Verständnis der folgenden Herleitungen brauchst Du Kenntnisse über Differentialrechnung (Ableitungen). Falls Du im Mathematikunterricht noch nichts davon gehört hast, schau' Dir einfach nur die Ergebnisse an (Funktionen $U(t)$).
a) Ladevorgang
 Wir suchen die Funktion $Q(t)$, die beschreibt, wie sich die Ladung des Kondensators mit der Zeit ändert
Beim Ladevorgang sei der Kondensator anfangs entladen, d.h.
$$Q(0) = 0$$
Für die Spannung $U(t)$, die am Kondensator anliegt, gilt
$$U(t) = U_0 - R\cdot I(t) = U_0 - R\cdot\dot Q(t)$$
Wegen $Q = C \cdot U$ gilt
$$Q(t) = C\cdot ( U_0 - R\cdot\dot Q(t))$$
Dabei bedeutet der Punkt über $\dot Q(t)$, dass $Q(t)$ hier nach der Zeit abgeleitet wird. Diese Art von Gleichung, bei der eine Funktion und auch ihre Ableitung vorkommen, nennt man Differentialgleichung. Gesucht ist die Funktion, die für alle Werte von $t$ diese Gleichung erfüllt.
Wir suchen die Funktion $Q(t)$, die beschreibt, wie sich die Ladung des Kondensators mit der Zeit ändert
Beim Ladevorgang sei der Kondensator anfangs entladen, d.h.
$$Q(0) = 0$$
Für die Spannung $U(t)$, die am Kondensator anliegt, gilt
$$U(t) = U_0 - R\cdot I(t) = U_0 - R\cdot\dot Q(t)$$
Wegen $Q = C \cdot U$ gilt
$$Q(t) = C\cdot ( U_0 - R\cdot\dot Q(t))$$
Dabei bedeutet der Punkt über $\dot Q(t)$, dass $Q(t)$ hier nach der Zeit abgeleitet wird. Diese Art von Gleichung, bei der eine Funktion und auch ihre Ableitung vorkommen, nennt man Differentialgleichung. Gesucht ist die Funktion, die für alle Werte von $t$ diese Gleichung erfüllt.
Man kann zeigen, dass
$$Q(t) = C\cdot U_0\cdot(1-e^{\frac{-t}{R\cdot C}})$$
diese Differentialgleichung löst. Wegen $U = Q/C$ gilt für den zeitlichen Verlauf der Spannung am Kondensator:
$$U(t) = U_0 \cdot(1-e^{\frac{-t}{R\cdot C}})$$
Für unsere Schaltung oben ($R = 10\,\mathrm{k\Omega}$, $C = 470\,\mathrm{\mu F}$, $U_0 = 5\,\mathrm V$) erhalten wir als Zeitkonstante
$$R\cdot C = 10\,\mathrm{k\Omega}\cdot 470 \,\mathrm{\mu F} = 4700\cdot 10^{-3}\,\mathrm{\Omega F} = 4700\cdot 10^{-3}\,\mathrm{\frac V A \cdot \frac{As}{V}} = 4,7\,\mathrm s$$
Damit ergibt sich für den zeitlichen Verlauf der Spannung:
$$U(t) = 5\,\mathrm V \cdot (1-e^{\frac{-t}{4,7\,\mathrm s}})$$
Hier ein Ausschnitt des Graphen (x-Achse: t in s, y-Achse: U in V):

b) Entladevorgang
 Wir suchen die Funktion $Q(t)$, die beschreibt, wie sich die Ladung des Kondensators mit der Zeit ändert
Beim Entladevorgang sei der Kondensator anfangs geladen, d.h.
$$Q(0) = C\cdot U_0$$
Da sich beim Entladen keine Stromquelle im Stromkreis befindet, ist die Spannung $U(t)$ am Kondensator gleich groß wie die Spannung am Widerstand, d.h.
$$U(t) = R\cdot I(t) = R\cdot\dot Q(t)$$
Wegen $Q = C \cdot U$ gilt
$$Q(t) = C\cdot R\cdot\dot Q(t)$$
Dabei bedeutet der Punkt über $\dot Q(t)$, dass $Q(t)$ hier nach der Zeit abgeleitet wird. Diese Art von Gleichung, bei der eine Funktion und auch ihre Ableitung vorkommen, nennt man Differentialgleichung. Gesucht ist die Funktion, die für alle Werte von $t$ diese Gleichung erfüllt.
Wir suchen die Funktion $Q(t)$, die beschreibt, wie sich die Ladung des Kondensators mit der Zeit ändert
Beim Entladevorgang sei der Kondensator anfangs geladen, d.h.
$$Q(0) = C\cdot U_0$$
Da sich beim Entladen keine Stromquelle im Stromkreis befindet, ist die Spannung $U(t)$ am Kondensator gleich groß wie die Spannung am Widerstand, d.h.
$$U(t) = R\cdot I(t) = R\cdot\dot Q(t)$$
Wegen $Q = C \cdot U$ gilt
$$Q(t) = C\cdot R\cdot\dot Q(t)$$
Dabei bedeutet der Punkt über $\dot Q(t)$, dass $Q(t)$ hier nach der Zeit abgeleitet wird. Diese Art von Gleichung, bei der eine Funktion und auch ihre Ableitung vorkommen, nennt man Differentialgleichung. Gesucht ist die Funktion, die für alle Werte von $t$ diese Gleichung erfüllt.
Man kann zeigen, dass
$$Q(t) = C\cdot U_0\cdot e^{\frac{-t}{R\cdot C}}$$
diese Differentialgleichung löst. Wegen $U = Q/C$ gilt für den zeitlichen Verlauf der Spannung am Kondensator:
$$U(t) = U_0 \cdot e^{\frac{-t}{R\cdot C}}$$
Für unsere Schaltung oben ($R = 10\,\mathrm{k\Omega}$, $C = 470\,\mathrm{\mu F}$, $U_0 = 5\,\mathrm V$) erhalten wir als Zeitkonstante
$$R\cdot C = 10\,\mathrm{k\Omega}\cdot 470 \,\mathrm{\mu F} = 4700\cdot 10^{-3}\,\mathrm{\Omega F} = 4700\cdot 10^{-3}\,\mathrm{\frac V A \cdot \frac{As}{V}} = 4,7\,\mathrm s$$
Damit ergibt sich für den zeitlichen Verlauf der Spannung:
$$U(t) = 5\,\mathrm V \cdot e^{\frac{-t}{4,7\,\mathrm s}}$$
Hier ein Ausschnitt des Graphen (x-Achse: t in s, y-Achse: U in V):