Table of Contents
Binärzähler (binary counter)
Wie ein Binärzähler aus Flipflops aufgebaut wird, hast Du im Kapitel "JK-Flipflop 74HCT107" schon kennengelernt. Jetzt verwenden wir dafür den Schaltkreis 74HCT 393, der zwei Vier-Bit-Binärzähler (also insgesamt 8 Flipflops) enthält. Beim Beschalten musst Du auf folgendes achten:
- Der Zähler reagiert nur dann auf das Clock-Signal, wenn Du den Pin “Reset” explizit mit Ground verbindest. Lässt Du den PIN offen, so hat dies dieselbe Wirkung wie “HIGH”, d.h. alle Ausgänge Q0 - Q3 werden auf low gesetzt und der Zähler reagiert nicht auf Änderungen am Clock-Eingang.
- Der Clock-Eingang ist invertiert. Das bedeutet, dass jeweils bei einer fallenden Flanke (Übergang von HIGH auf LOW) um eins weitergezählt wird.
- Du kannst die beiden 4-Bit-Zähler leicht zu einem 8-Bit-Zähler kombinieren. Dazu musst Du nur den Ausgang 1 Q3 des ersten Zählers mit dem Clock-Eingang des zweiten Zählers verbinden.
Falls Du das Binär-Zahlensystem noch nicht kennst oder eine kleine Erinnerung brauchst, oder einfach nur in Erinnerungen an Deine Kindheit schwelgen willst, schau' Dir den folgenden kurzen Sachfilm aus der Sendung mit der Maus an:
1. 4-Bit-Zähler mit LEDs
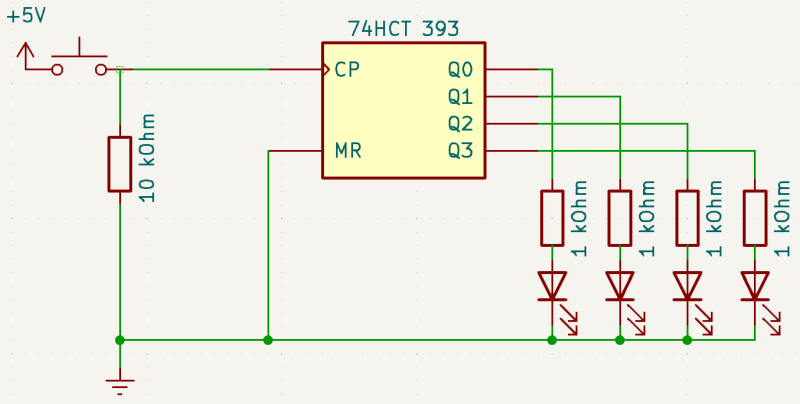
Im Schaltplan oben ist CP der invertierte Clock-Eingang und MR der Reset-Eingang.
Jedesmal, wenn Du den Taster loslässt, hat dies einen Übergang von HIGH auf LOW am CLock-Eingang des Zähler zur Folge, so dass dieser im Binärsystem um eins weiterzählt.
Folgendes fällt auf:
- a) Manchmal zählt der Zähler beim Loslassen des Tasters nicht nur um 1 weiter, sondern gleich mehrfach. Woran könnte das liegen? Was lässt sich dagegen tun?
(Hier findest Du die Antwort auf diese Frage.) - b) Ich habe die Schaltung bei mir zuhause aufgebaut und mit dem Steckernetzteil gespeist. Dabei habe ich folgende Beobachtung gemacht: Wenn der Clock-Eingang völlig unbeschaltet war, begann der Zähler sehr schnell von selbst zu zählen. Ist es bei Deiner Schaltung genauso? Kannst Du die Zählfrequenz ermitteln? Woher kommt dieser Effekt?
Tipp: Zum Ergründen dieses Phänomens könntest Du auch das Oszilloskop verwenden.
Nutze den Taktgeber aus dem Kapitel "555 Timer" oder einen Funktionsgenerator, um die Schaltung statt des Tasters mit einem periodischen Clock-Signal zu speisen.
VORSICHT:
Stecke unbedingt vorher den Taster und den Pull-Down-Widerstand ab!
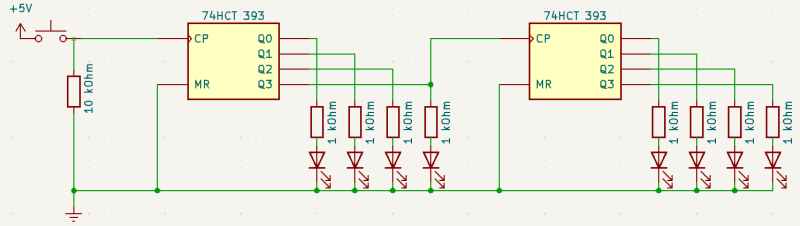
2. Erweiterung auf 8 Bit
Immer dann, wenn die vierte LED ausgeht (d.h. die 8'er Stelle des Zählers von 1 zu 0 übergeht), muss die 16'er-Stelle ihren Zustand ändern. Das wird erreicht, indem der vierte Ausgang des ersten Zählers mit dem invertierten Clock-Eingang des zweiten Zählers verbunden wird.
3. Ansteuerung eines 7-Segment-Displays
Ein 7-Segment-Display besteht aus 7 LEDs für die Segmente einer Ziffer sowie einer 8. LED für den Dezimalpunkt (DP). Es gibt diese Displays grundsätzlich in zwei verschiedenen Varianten:
- Common Cathode: Die Minuspole aller 8 LEDs sind mit den beiden COM-Pins verbunden, die Pluspole mit den Ausgängen a - g bzw. DP.
- Common Anode: Die Pluspole aller 8 LEDs sind mit den beiden COM-Pins verbunden, die Minuspole mit den Ausgängen a - g bzw. DP.
Wir arbeiten mit Common Cathode-Displays. Damit beispielsweise die Ziffer 2 aufscheint, müssten wir das 7-Segment-Display also folgendermaßen beschalten:
4. 7-Segment-Display am Binärzähler
Was liegt näher, als ein 7-Segment-Display an einen Binärzähler anzsuschließen, damit es dessen Ausgabe als Dezimalzimmer anzeigt?
Leider ist das nicht so einfach möglich, da die Ausgänge des Binärzählers den Stellen der Binärzahl entsprechen, die Eingänge des 7-Segment-Displays aber den Strichen innerhalb der Dezimalziffern. Wie bringen wir das zusammen?
Schauen wir uns dazu mal nur das linke untere Segment (e) an:
Dieses Segment muss genau dann leuchten, wenn die Ziffern 0, 2, 6, oder 8 angezeigt werden, also bei den Binärzahlen 0000, 0010, 0110 und 1000, nicht aber bei den Binärzahlen 0001, 0011, 0100, 0101, 0111. Die vier Binärstellen entsprechen (in dieser Reihenfolge) den Ausgängen $Q_3$, $Q_2$, $Q_1$ und $Q_0$ des Binärzählers.
Schaut man genau hin, so findet man die Regel:
Das Segment e soll dann und nur dann leuchten, wenn die Zahl gerade und gleichzeitig nicht 4 ist.
Gerade ist die Zahl genau dann, wenn $Q_0$ low ist. Unter den geraden Zahlen kann man die 4 ausschließen, wenn man sicherstellt, dass nicht gleichzeitig $Q_2$ HIGH und $Q_1$ LOW ist. Wir können die Aussage also formalisieren zu:
Das Segment e soll dann und nur dann leuchten, wenn $(\mathrm{nicht}\ Q_0)\ \mathrm{und}\ \mathrm{nicht}\ (Q_2\ \mathrm{und}\ (\mathrm{nicht}\ Q_1))$ HIGH ist.
Überprüfen wir kurz anhand einer Tabelle, ob unsere Überlegung richtig ist:
| Ziffer | binär $Q_3Q_2Q_1Q_0$ | $\mathrm{nicht}\ Q_0$ | $Q2\ \mathrm{und}\ (\mathrm{nicht}\ Q_1))$ | $(\mathrm{nicht}\ Q_0)\ \mathrm{und}\ \mathrm{nicht}\ (Q_2\ \mathrm{und}\ (\mathrm{nicht}\ Q_1))$ |
|---|---|---|---|---|
| 0 | 0000 | HIGH | LOW | HIGH |
| 1 | 0001 | LOW | LOW | LOW |
| 2 | 0010 | HIGH | LOW | HIGH |
| 3 | 0011 | LOW | LOW | LOW |
| 4 | 0100 | HIGH | HIGH | LOW |
| 5 | 0101 | LOW | HIGH | LOW |
| 6 | 0110 | HIGH | LOW | HIGH |
| 7 | 0111 | LOW | LOW | LOW |
| 8 | 1000 | HIGH | LOW | HIGH |
| 9 | 1001 | LOW | LOW | LOW |
⇒ Passt alles!
Wollen wir diesen Term als Schaltung realisieren, so brauchen wir drei NICHT-Gatter und zwei UND-Gatter:
Kostengünstig produzieren
Stell' Dir vor, Du arbeitest als Ingenieurin in einer Firma, die 100 000 der obigen Schaltungen produzieren möchte. Dazu sind 100 000 Bausteine 74HCT14 (je 4 UND-Gatter) und 100 Bausteine 74HCT08 (je 6 invertierende Schmitt-Trigger)nötig. Viele Gatter in den Bausteinen werden gar nicht genutzt. Geht das vielleicht besser?
Ansatz: Umformen des Logikterms
So, wie man arithmetische Terme oft vereinfachen kann kann (Assoziativgesetz, Kommutativgesetz, Distributivgesetz, …, erinnerst Du Dich?), kann man auch Logikterme (“Boolesche Terme”) umformen. Das entsprechende Fachgebiet der Mathematik heißt Boolesche Algebra. Wir nutzen eines der de Morganschen Gesetze, um den obigen Term zu vereinfachen: “nicht(A und B) = nicht A oder nicht B”
$$(\mathrm{not}\ Q_0) \mathrm{and}\ \mathrm{not}\ \bigl(Q_2\ \mathrm{and}\ \left(\mathrm{not}\ Q_1\right)\bigr) = $$
$$\mathrm{not}\ \Bigl(Q_0\ \mathrm{or}\ (Q_2\ \mathrm{and}\ \left(\mathrm{not}\ Q_1\right)\bigr)\Bigr) = $$
$$\mathrm{not}\ \Bigl(Q_0\ \mathrm{or}\ \mathrm{not}\bigl((\mathrm{not}\ Q_2)\ \mathrm{or}\ Q_1\bigr)\Bigr)$$
Sieht noch nicht richtig einfach aus, oder? Verwendet man aber den NOR-Operator (A NOR B ist definiert als NOT (A OR B)), so vereinfacht sich das zu:
$$Q_0\ \mathrm{nor}\ \Bigl(\mathrm{not}\ \bigl((\mathrm{not}\ Q_2)\ \mathrm{or}\ Q_1\bigr)\Bigr) = $$
$$Q_0\ \mathrm{nor}\ \bigl((\mathrm{not}\ Q_2)\ \mathrm{nor}\ Q_1\bigr)$$
Da man aus einem NOR-Gatter durch Zusammenschalten beider Eingänge auch ein NICHT-Gatter bauen kann, kommt die entsprechende Schaltung also mit drei NOR-Gattern aus.
Damit reicht uns ein einziger 74LS02-Baustein!
Hier ist die entsprechende Schaltung, probier' sie aus!
So wie die obige Schaltung lassen sich auch entsprechende Schaltungen für die anderen 6 Segmente des Displays finden. Probiere es zur Übung für eines der anderen Segmente selbst aus!
Sicher wirst Du Dir schon gedacht haben, dass es wohl ein IC gibt, dass alle sieben Schaltungen enthält…
7-Segment-Decoder 74HCT4511
Der 74HCT4511 nimmt an seinen Eingängen A - D eine 4-Bit BCD-encodierte Ziffer entgegen und gibt an seinen Ausgängen a - g die Belegung der LEDs einer 7-Segmentanzeige so aus, dass sie die Ziffern 0 - 9 korrekt darstellt. Zu den weiteren Eingängen:
- Direkt hinter den Eingängen A - D befindet sich je ein D-Flipflop, erst dahinter kommt der eigentliche Decoder. Liegt $\bar{LE}$ (“latch enable”) auf LOW, so wird das Signal der Eingänge A - D zum Decoder durchgereicht und in den Flipflops gespeichert. Liegt es auf HIGH, so liegen am Decoder die in den Flipflops gespeicherten Werte an.
- Liegt $\bar{LT}$ (“lamp test”) auf low, so liegen alle Ausgänge a - g auf HIGH, unabhängig vom Zustand der anderen Eingänge.
- $\bar{BL}$ (“ripple blanking”) dient der Vornullenunterdrückung. Liegt es auf Low, so liegen auch alle Ausgänge auf LOW, unabhängig von den anderen Eingängen.
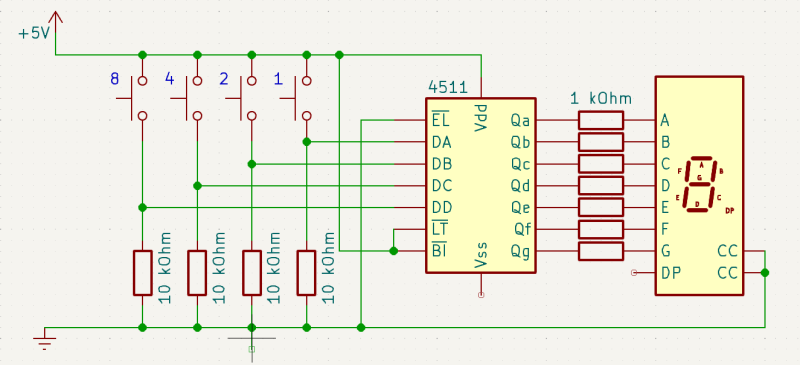
Hier eine einfach Testschaltung für den 74HCT4511:
Aufgaben:
- Schließe ein 7-Segment-Display mit Hilfe des 74HCT4511 an den Zähler oben an!
- Was passiert, wenn der Zähler die 9 überschreitet? Schau' Dir das Datenblatt zum 74HCT4511 an und erkläre das Verhalten! Wie könntest Du erreichen, dass er dann wieder bei 0 beginnt? Baue eine entsprechende Schaltung!
- Der 74HCT390 ist ein BCD-Zähler, der so beschaltet werden kann, dass er beim Zehnerübergang auf 0 zurückgeht und einen Clock-Puls für die nächste Zehnerstelle ausgibt. Schau' Dir das Datenblatt genau an und baue damit einen 2-stelligen Dezimalzähler, der von 0 bis 99 zählt!
Hier geht's zur Lösung von Aufgabe 3.
